Local Laplacian Filtering : Image Detail Enhancement and Tone Mapping

Introduction

本篇利用了標準的Laplacian pyramid，藉由操作修改residual layer來達到detail enhancement與tone mapping的效果。想當然是halo free；此外的特色是no optimization、no gradient domain manipulation，所以適用實作和加速。上圖則是激動人心的差異!

 

 

這邊我實作了一個簡易版的 javascript demo ，速度很慢，不要太期待。

 

 

1. Laplacian Pyramid

1.1 Build Laplacian pyramid

參考[4]中敘述，特別提醒residual是當前image減去downsample再upsample的影像，而非減去Gaussian blur後的影像。

 

pyramid 由大到小分別是0到\(n-1\)層，第\(n-1\)層是一個 low pass 影像，其餘則是不同scale 的 high pass 部分。特別注意 downsampe 是先行 low pass filter 後跳點縮小，若沒有先 low pass 直接縮小，可能會產生較嚴重的aliasing。

下面是建立 Laplacian pyramid的過程，其中\(L_{i}\)與\(G_{i}\)分別表第\(i\)層的Laplacian pyramid 與 Gaussian pyramid

1. \(G_{i+1}=downsample(G_{i})\)
2. \(G^{‘}_{i}=upsample(G_{i+1})\)
3. \(L_{i}=G_{i}-G^{‘}_{i}\)

1.2 Reconstruction from Laplacian pyramid

重建影像的方法很直覺，由第\(n-1\)層做upsampling後加上第\(n\)層的residual，直到原影像大小為止。

\[G_{i}=upsample(G_{i+1})+L_{i}\]

1.3 Accurate Image Up-sampling and Down-sampling in Pyramid-based Algorithm

2. Local Detail Enhancement and Tonemapping

remapping function \(r(i)\)的想法很簡單，在local區域求mean \(g_{0}\)，得到中間灰\(g_{0}\pm{\sigma_{r}}\)、亮部大於\(g_{0}+\sigma_{r}\)、暗部小於\(g_{0}-\sigma_{r}\)，三種強度分布。對中間灰的部分套用 S-curve強化，亮暗部則是線性壓制強度。

\[
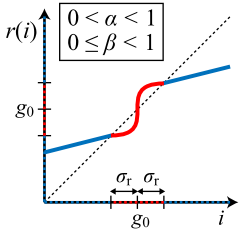
r(i)=\begin{matrix}r_{d}(i)&,\left|d(i)\right|\le\sigma_{r}\\r_{e}(i)&,\left|d(i)\right|>\sigma_{r}\end{matrix}
\]

• \(d(i)=i-g_{0}\)
• \(r_{d}(i)=g_{0}+sign(d(i))\sigma_{r}\left(\frac{\left|d(i)\right|}{\sigma_{r}}\right)^\alpha\)
• \(r_{e}(i)=g_{0}+sign(d(i))\beta(\left|d(i)\right|-\sigma_{r})+\sigma_{r}\)

其中\(r_{d}(i)\)與\(r_{e}(i)\)分別表中間灰與亮暗部的轉換。\(r_{d}(i)\)利用gamma correction的方式由[0 1]到[0 1]的一個S型的強化曲線；\(r_{e}(i)\)則是利用\(\beta\)線性調整強度。

實作上這部分可以將減去\(g_{0}\)的絕對值建表加速，而後再補上sign，可以省去很多計算。

2.1 Eliminate Noise

對於 local enhancement 而言，在 uniform 的區域如藍天，往往會enhance noise，因為在平坦區域的 local mean \(g_{0}\) 使 noise 落在中間灰的區域，進而被強化。對於這種地方我們可以考慮使用一些判斷，使\(r(i)\)退化成接近線性輸出，甚至是逆s-curve，進而在保留影像結構的情況下壓抑noise。在[2]中有提及其數學等價於bilaterial filtering。

• 每一層 residual \(L_{i}\) manipulation 可以帶入 不同的 \(\alpha_{i}\)
• 每個點可以使用不同的 \(\alpha_{i,(x,y)}\)，並且\(\alpha_{i,(x,y)}\) 在空間的變化是平滑的

 

3. Coordinate Transfer between Pyramid Layers

這部分可為本論文最困難的地方，無論是downsample、upsample或residual sampling，我們都必須要保證座標是精準轉換的。否則將發生如殘影、模糊等意外情形，嚴重挫折玩家信心。幾個重點提醒:

• downsample影像大小能夠大就盡量大，保留較多資訊，\(round(3)=2\)

4. Algorithm

• For every scale image \(G_{i}\) and every pixel \(G_{i}(x, y)\) where \({i}\le{n-2}\)
  • Enhance locally good contrast image using remapping function \(r(G_{i}(x, y))\).
  • Build local Laplacian pyramid of local image.
  • Replace the corresponded residual by enhanced residual in global Laplacian pyramid.
• End for
• Reconstruct final image from enhanced Laplacian pyramid.

%% naive O(N^2) version for reference
G = gaussian_pyramid(I);
L = laplacian_pyramid(zeros(size(I))); 
for level = 1:length(L)-1
    for y = 1:size(G{level},1)
        for x = 1:size(G{level},2)
            g0 = G{level}(y,x,:);
            Iremap = r(I,g0);
            Lremap = laplacian_pyramid(Iremap,level+1);
            L{level}(y,x,:) = Lremap{level}(y,x,:);
        end
    end
end
L{end} = G{end};
R = reconstruct_laplacian_pyramid(L);

5. Speedup Algorithm

5.1 Speedup by multi-pyramids with different mean values

基於”space-time trade-off”的原理，這個方法就是拿記憶體換時間，非常瘋狂，但是已經應用在新版的 Adobe Lightroom.

在原本的 algorithm 中，local enhancement 是針對不同 local mean \(g_{0}\) 做的，共需要影像pixel個數這麼多次的 full image pyramid 計算。若我們可以合併不同 local enhancement 的 pyramid 計算，速度就可以大幅增加 (論文中表示約為50倍加速)。

 

離散取樣\(N\)個local means，計算\(N\)個由全圖取樣的 Laplacian pyramid。在 residual manipulation時就取相近 local mean 得到的  residual 即可 (Nearest Neighbor method)。而\(N\)的大小控制了記憶體使用量和畫質，如下圖：

實作上，可能需要一個 histogram 來分析 intensity 的分布，藉此來分配 local means 的分布，不一定是 uniform-spaced 的取樣，才可以在極值附近有較佳的結果，並且\(N\)也不會太大。

5.1.1 linear residual interpolation

使用 nearest neighbor 在 uniform 區域的顆粒感嚴重，所以我們將取離 local mean 最近的兩組 pyramid 取樣做 linear interpolation，藉此消彌明顯的顆粒感。

5.1.2 Gaussian weighted residual

但[2]中提到的 linear interpolation 的結果仍不盡完美，在 uniform 的區域仍有不自然的漸層產生。這邊我將其延伸，擴大 blending 取樣的 pyramid 組數。以 nearest neighbor 找到的 pyramid 為中心，前後各span \(k=2\) 組 pyramid，以 Gaussian-like 的 weighting 加權。

這邊使用\(weighting = \frac{1}{9}\{1, 2, 3, 2, 1\}\)

下圖展示 Gaussian weighted 的方式，即使在\(N\)不大時也能有不錯的品質。

5.2 Speedup by Local Laplacian Pyramid

 

Reference

1. Local Laplacian Filters: Edge-aware Image Processing with a Laplacian Pyramid, SIGGRAPH 2011
2. Fast Local Laplacian Filters: Theory and Applications, SIGGRAPH 2014
3. Gradient domain high dynamic range compression, SIGGRAPH 2002
4. The Laplacian Pyramid as a Compact Image Code, IEEE TRANSACTIONS ON COMMUNICATIONS, 1983